Matematiikan historiassa yksi kiehtovimmista tarinoista liittyy piin (π) eli ympyrän kehän ja halkaisijan suhteen likiarvojen etsintään. Muinaiset kulttuurit tunsivat piin ja käyttivät erilaisia menetelmiä sen määrittämiseen. Yksi tunnetuimmista ja varhaisimmista piin likiarvoista oli 22/7, joka tunnettiin jo vähintään antiikin aikoina.

Varhaisimmat dokumentoidut yritykset määrittää piin arvo löytyvät Babyloniasta ja muinaisesta Egyptistä yli kolmen ja puolen tuhannen vuoden takaa. Babyloniassa käytetty likiarvo 25/8 (3.125) ja Egyptissä käytetty 256/81 (3.1605) olivat ensimmäisiä yrityksiä arvioida tätä salaperäistä lukua.

Raamatussa mainitaan rituaaliastia, joka tunnetaan ”Molten Sea” nimellä, ja sen mitat annetaan 1. Kuningasten kirjassa (7:23). Astian halkaisija on 10 kyynärää ja sen ympärysmitta 30 kyynärää, mikä antaa piille likiarvon 3. Tämä on huomattavan suuri ero oikeasta piin arvosta, joka varmasti olisi huomattu käytännöllisissä laskuissa. Jos otetaan huomioon astian kämmenen paksut kaarevat reunat, arvio tarkentuu ja lähenee oikeaa piin arvoa, koska astian sisäpinnan ja ulkopinnan mukaiset kehän mitat antavat eri arvon piille.

22/7 Arkhimedeen ansiota?

Yksi tunnetuimmista nimistä piin historiassa on kreikkalainen matemaatikko Arkhimedes, joka eli 300-luvulla eaa. Arkhimedes käytti geometrisia monikulmioita ympyrän sisällä ja ulkopuolella ja päätyi arvoihin 3 10/71 (noin 3.1408) ja 3 1/7 (noin 3.1429), joista jälkimmäinen tunnetaan nykyään muodossa 22/7.

On kuitenkin mahdollista, että tämä suhde oli tiedossa jo ennen Arkhimedesta, vaikkei meille ole säilynyt kirjallista mainintaa asiasta. Arkkitehtuuri voi paljastaa kirjoittamattomia mysteereitä. Yksi esimerkeistä löytyy Gizan pyramidin mittasuhteista Egyptistä, nykyisestä Kairosta. Suuren pyramidin, joka tunnetaan myös nimellä Kheopsin pyramidi, korkeus on noin 146,6 metriä ja sen sivujen pituus on noin 230,4 metriä. Jos jaamme pyramidin sivujen (2) pituuden sen korkeudella, saamme likimääräiseksi arvoksi noin 3,143247, joka on lähellä arvoa 22/7. Suhde on ilmeinen, kun tunnetaan pyramidin mitat muinaisten egyptiläisten kubitteina eli kyynärinä. Pyöristettyinä korkeus 140 kyynärää on 7×20 ja leveys 220 eli 22×10 kyynärää. Tästä näkyy hyvin 22 ja 7 suhde.

Tunsivatko muinaiset egyptiläiset piin ja käyttivät sitä rakennustekniikoissaan? Tämä tarkoittaisi, että pii olisi tunnettu jo yli 2000 vuotta ennen Arkhimedesta, joka olisi sensaatiomaista, jos se voitaisiin vahvistaa jollain muulla vertaisella tavalla. Vai oliko tämä vain sattumaa ja tahaton seuraus tietyistä mitoista ja mittasuhteista, joita he pitivät suuressa kunniassa, kuten kuninkaallista kyynärää, joka oli seitsemän kämmentä kuuden sijasta? 

Lukua seitsemän on pidetty tunnetusti pyhänä lukuisissa kulttuureissa, joka saattaisi selittyä 22/7 suhdeluvun nimittäjän merkityksestä ja siirtymisestä erilaisten tarinoiden ja traditioiden kautta aina viime vuosisadoille saakka. Toki ~7 (5 x neliöjuuri 2) on myös lävistäjän mitta, jos neliön sivu on 5. Lisäksi kahden toisiaan keskeltä leikkaavien ympyrän muodostaman Vesica Pisciksen eli ovaalin muotoisen leikkauskuvion korkeuden ollessa 6, ovat ympyröiden halkaisijat ~7.

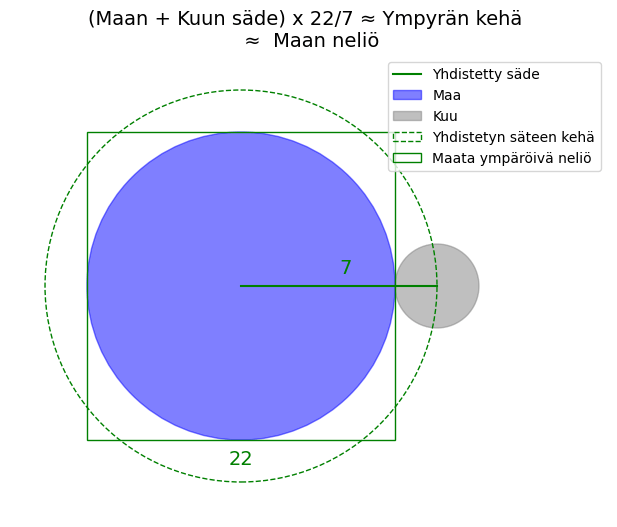
Toinen mielenkiintoinen yksityiskohta liittyy Maan ja Kuun mittasuhteisiin. Maan säde on noin 6 371 km ja Kuun säde noin 1 737 km. Yhteensä nämä ovat noin 8 108 km. Kun verrataan tätä summaa Maan ympärille piirretyn neliön sivun pituuteen, joka olisi kaksinkertainen Maan säde eli noin 12 742 km, saadaan suhdeluku, joka on noin 3,1419. Se muistuttaa hyvin lähelle piin arvoa. Jälleen kerran mitat ovat ilmeisempiä, jos metrien sijasta käytetään maileja (yhteinen säde 5040 eli 7×720, maan neliö 7920 eli 22×360 mailia).

Näin 22/7 suhde toimii ympyrän ja neliön mittojen likimääräisenä yhtenäistäjänä. Onko muita vastaavia sattumia maailmassa, joissa muinoin merkitykselliset luvut löytyvät näin yllättävistä luonnon ja kosmoksen yhteyksistä?

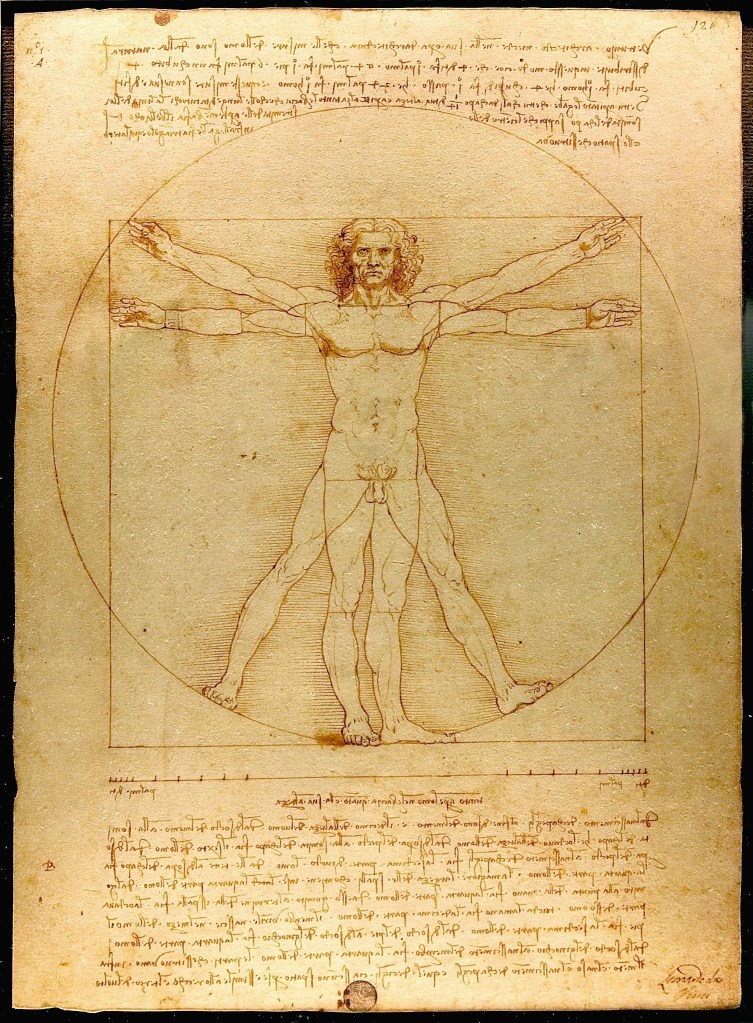
Yksi tunnetuista anatomisista tutkielmista on Leonardo da Vincin Vitruvian Mies (1490 jaa.), jossa ihmisen ympärille piirretyt ympyrä ja neliö hyödyntävät mahdollisesti tätä samaa ikuisen taivaallisen ympyrän ja maallisen neliön suhdetta. Da Vincia edeltävä aikalainen, Dante kuvaa Jumalaisessa näytelmässä (1321 jaa.) Helvetin seitsemännessä piirissä tuskailevaa geometrikkoa, joka ei millään saa ympyräänsä neliöityä, eli tämän tehtävän mahdottomuus on jossain mielessä, intuitiivisesti jo ehkä aavisteltu.

Ympyrän neliöiminen

Ympyrän neliöiminen, eli ongelma, jossa pyritään rakentamaan neliö, jonka sivujen pituus (tai vaihtoehtoisesti pinta-ala) on sama kuin annetun ympyrän kehä, on yksi klassisista geometrisista haasteista, joka on periytynyt meille antiikista. Vaikka se osoitettiin mahdottomaksi tarkasti rakentaa pelkästään kiinteän harpin ja viivoittimen avulla 1800-luvulla, on olemassa muitakin tapoja ratkaista tämä ongelma.

Hyperbolisessa geometriassa, jossa taso on kaareva eikä tasainen, ympyrän neliöiminen voidaan toteuttaa erilaisilla laskelmilla ja menetelmillä, jotka eivät päde euklidisessa geometriassa. Lisäksi muuntuvaa harpin pituutta hyödyntämällä voidaan konstruoida neliö ympyrän kanssa vastaavilla pinta-aloilla. Origamigeometriassa, eli paperintaittelun matematiikassa, on mahdollista taitella paperi niin, että saadaan aikaan tarkka neliö, jonka pinta-ala vastaa ympyrän pinta-alaa. Gary Choi, MIT:n sovelletun matematiikan tutkija, on osoittanut, että tarkemmin ottaen kirigamitekniikka mahdollistaa paperin muodon muuttamisen käsittelyn aikana, hyödyntäen leikkausten luomia tyhjiä tiloja.

Nykyään tiedämme, että pii on transsendentti irrationaaliluku, mikä tarkoittaa, että sen desimaalit jatkuvat ikuisesti ilman säännöllistä jaksoa. Piin ensimmäiset desimaalit ovat 3.141593. 22/7 antaa arvoksi 3.142857, mikä on suhteellisen lähellä todellista arvoa. On oikeastaan harvinaista, että näin pienillä kokonaisluvuilla päästään niin suureen likiarvotarkkuuteen.

22/7-päivää vietetään ympäri maailmaa epävirallisena piin päivänä 22. heinäkuuta. Tämä juhla on hauska vastine viralliselle piin päivälle, joka on 14. maaliskuuta (3/14). Piin-päivinä matematiikan harrastajat nauttivat piirasleivonnaisia (englanniksi pie) ja järjestävät leikkimielisiä visailuja, joissa muistellaan muinaisilta kulttuureilta meille välittyneitä älyllisiä pähkinöitä.

Hyvää muinaisen piin päivää!